Problem Józefa Flawiusza (także: permutacja Józefa Flawiusza) – problem teoretyczny z zakresu kombinatoryki. Często rozważany w informatyce. W ogólnej wersji problem brzmi następująco: na okręgu ustawiamy n obiektów, następnie eliminujemy co k-ty obiekt, tak długo, aż zostanie tylko jeden. Należy wskazać obiekt, który pozostanie.
Pierwszym, który przekształcił tę historię w problem matematyczny, miał być szesnastowieczny francuski matematyk Claude Gaspard Bachet de Méziriac. Według niego, ustawieni w okrąg żołnierze mieli eliminować co trzeciego spośród siebie. Po Bachecie historia ta była wielokrotnie powtarzana ze zmieniającymi się szczegółami – przykładowo Kaplansky podaje, że powstańców było 40 (wliczając Flawiusza), a eliminowano co siódmego. Flawiusz, postawiony przed problemem, miał szybko policzyć, gdzie musi się ustawić, by przeżyć.
Inne źródło podaje, że uczestników było łącznie 41, a Flawiusz i wtajemniczony przez niego powstaniec ustawili się odpowiednio na 31. i 16. pozycji. W tej wersji problemu należy wyznaczyć dwóch ostatnich ludzi, którzy pozostaną przy życiu. Wersja przedstawiona w Matematyce konkretnej zakłada, że zabijany jest co drugi uczestnik. Jest to jedyna wersja problemu, dla której udowodniono istnienie wzoru jawnego.
Istnieje też pokrewny problem, który został wymyślony w średniowieczu. 15 Turków i 15 chrześcijan płynie statkiem w trakcie sztormu. Kapitan stwierdza, że, aby uratować statek, połowa pasażerów musi go opuścić. Pasażerowie stają w kręgu i co dziewiąty skacze do morza. W tej wersji należy znaleźć pozycje, na których mają ustawić się chrześcijanie, by przeżyć
Dla k=2 istnieje wzór jawny, a dla pozostałych k istnieją algorytmy rozwiązujące problem między innymi w złożonościach czasowych O(n) i O(k log n)
Niech n oznacza początkową liczbę osób w kręgu, a k krok w każdej iteracji (po każdej egzekucji k-1 osób po poprzednio wybranej jest pomijanych, a k-ta zabijana). Osoby w kręgu numerowane są od liczbami naturalnymi od 1do n, a jako pierwszy zabijany jest uczestnik o numerze k.
dla k=2
Niech J(n) oznacza pozycję pozostałego uczestnika w sytuacji, gdy na początku było ich n.
Pierwsza runda wokół okręgu eliminuje wszystkich uczestników o numerach parzystych. Jeżeli n jest parzyste, to po tej rundzie sytuacja będzie o tyle podobna, że wciąż mamy do czynienia z parzystą liczbą uczestników, lecz o nieco zmienionych numerach. Zakładając, że zaczęliśmy z 2n uczestnikami, po pierwszej rundzie sytuacja wygląda tak, jakbyśmy zaczynali z n uczestnikami o podwojonych i zmniejszonych o 1 numerach. Otrzymujemy więc:
J(2n)=2J(n)-1 dla n>=1
Jeżeli zaczynamy z 2n+1 uczestnikami i wykonujemy jedną rundę, to uczestnik o numerze 1 jest eliminowany zaraz po uczestniku o numerze 2n. Ponownie zostajemy z n osobami, jednak tym razem ich numery są podwojone i powiększone o 1, a więc:
J(2n+1)=2J(n)+1 dla n>=1
Łącząc te równania z J(1)=1 otrzymujemy wzór rekurencyjny, który pozwala na policzenie J(n) w złożoności obliczeniowej O(log n). Można wykorzystać ten wzór do stablicowania funkcji J(n).

Można zaobserwować, że wartości da się zgrupować według kolejnych potęg 2, a kolejne grupy są ciągami liczb nieparzystych. Stąd otrzymujemy wzór
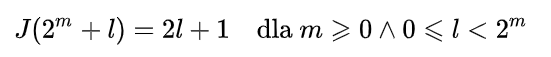
Wzór jawny
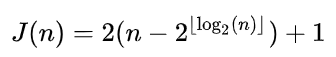
Można też udowodnić, że J(n) odpowiada obrotowi bitowemu n o jedno miejsce w lewo. Jeśli przedstawimy n w postaci dwójkowej:
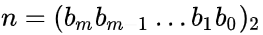
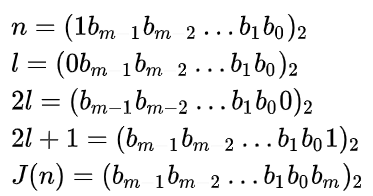
Przypadek ogólny
Problemem, który pozostaje otwarty, jest wyznaczanie J(n) w sytuacji, gdy k!=2. Rozwiązanie intuicyjne, działające w złożoności O(nk)polega na wykorzystaniu listy i przechodzeniu jej w koło, usuwając co k-ty odwiedzony element.
Opisano też rozwiązania, działające w O(nlog n) i wykorzystujące zamiast listy binarne drzewa poszukiwań.
Szybsze rozwiązanie, działające w złożoności O(n), przewiduje wykorzystanie programowania dynamicznego. Niech L(n) oznacza pozycję bezpieczną przy wybranym k. Jeżeli numerujemy, zaczynając od 1, to osoba o s pozycji od niej znajduje się na pozycji ((s-1) mod n). Gdy zabijemy osobę na k-tej pozycji, zostajemy z kręgiem złożonym z n-1 osób i zaczynamy odliczać od osoby, która w oryginalnym problemie stała na pozycji (k mod n)+1. Biorąc pod uwagę zmianę numeracji w nowym kręgu, otrzymujemy następującą rekurencję
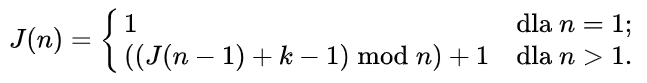
Przykład rozwiązania: