Odwrotna notacja polska (ONP, ang. reverse Polish notation, RPN) – sposób zapisu wyrażeń arytmetycznych, w którym znak wykonywanej operacji umieszczony jest po operandach (zapis postfiksowy), a nie pomiędzy nimi jak w konwencjonalnym zapisie algebraicznym (zapis infiksowy) lub przed operandami jak w zwykłej notacji polskiej (zapis prefiksowy). Zapis ten pozwala na całkowitą rezygnację z użycia nawiasów w wyrażeniach, jako że jednoznacznie określa kolejność wykonywanych działań.
Odwrotna notacja polska została opracowana przez australijskiego naukowca Charlesa Hamblina jako „odwrócenie” beznawiasowej notacji polskiej Jana Łukasiewicza na potrzeby zastosowań informatycznych. Hamblin sugerował, aby notację tę nazwać „Azciweisakul notation” (Notacja Azciweisakuł – „Łukasiewicza” pisane od tyłu).
Algorytm obliczenia wartości wyrażenia ONP
- Dla wszystkich symboli z wyrażenia ONP wykonuj:
- jeśli i-ty symbol jest liczbą, to odłóż go na stos,
- jeśli i-ty symbol jest operatorem to:
- zdejmij ze stosu jeden element (ozn. a),
- zdejmij ze stosu kolejny element (ozn. b),
- odłóż na stos wartość b operator a.
- jeśli i-ty symbol jest funkcją to:
- zdejmij ze stosu oczekiwaną liczbę parametrów funkcji(ozn. a1…an)
- odłóż na stos wynik funkcji dla parametrów a1…an
- Zdejmij ze stosu wynik.
Przykład 1
Wyrażenie w zapisie konwencjonalnym: 12+2×(3×4+10/5)
Wyrażenie ONP: 12 2 3 4 × 10 5 / + × +
Gdy wczytany element jest liczbą, to zapisuje się ją na stos. W przeciwnym wypadku należy wykonać działanie arytmetyczne na 2 ostatnich liczbach na stosie. Wartość wyrażenia znajduje się na stosie.
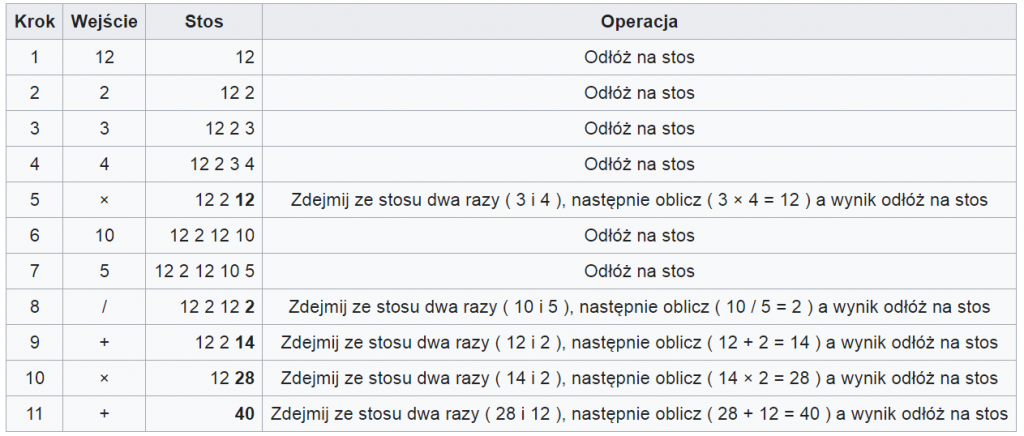
Wartość wyrażenia (zdejmij ze stosu ostatni element): 40
Przykład 2
Wyrażenie w zapisie konwencjonalnym: (1+2) × 4 + 5 − 3
Wyrażenie ONP: 5 1 2 + 4 × + 3 −
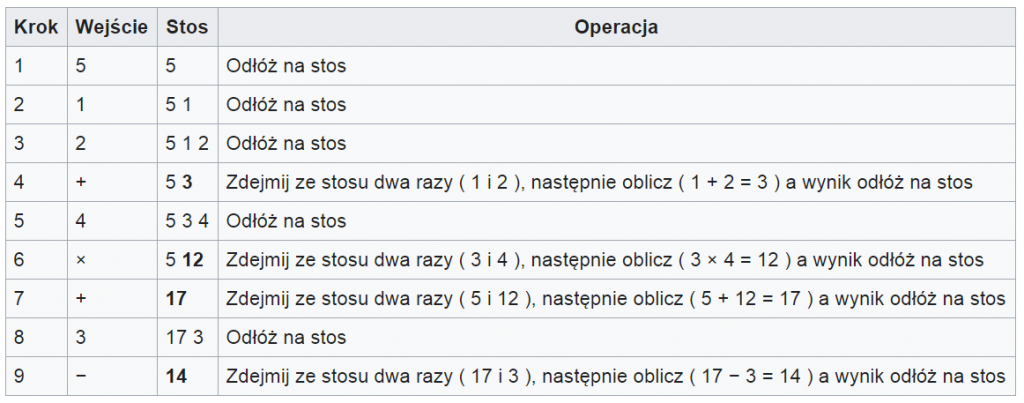
Wartość wyrażenia (zdejmij ze stosu ostatni element): 14
Algorytm konwersji z notacji infiksowej do ONP (rekurencyjny)
Funkcja ONP:
- Zdefiniowanie zmiennych char a, c.
(należy zdefiniować zmienne w funkcji ONP tak, aby za każdym razem gdy funkcja ONP się wykona, nastąpiło zapisanie wartości tych zmiennych w innym miejscu w pamięci. Gdyby zdefiniować te zmienne jako globalne, to nastąpiłoby błędne zastępowanie ich wartości, wartościami poprzednimi.)- Wczytaj znak z wejścia do zmiennej (c) i:
- Jeżeli przeczytany znak jest lewym nawiasem:
- Wywołaj funkcję ONP.
- Wczytaj znak z wejścia do zmiennej (a). (to zawsze powinien być operator)
- Wywołaj funkcję ONP.
- Ściągnij znak z wejścia nie zapisując go. (to zawsze powinien być prawy nawias)
- Wypisz zmienną (a) na wyjście.
- W przeciwnym wypadku wypisz wczytany znak (c).
Ten algorytm działa poprawnie jedynie dla wyrażeń, które mają pełne nawiasowanie np. (a+(b×c)).
Przykład (notacja infixowa):
(a+(b×c))
((a+b)×(z+x))
((a+t)×((b+(a+c))^(c+d)))
Po zamianie (w odwrotnej notacji polskiej):
abc×+
ab+zx+×
at+bac++cd+^×
Algorytm konwersji z notacji infiksowej do ONP
Edsger Dijkstra wymyślił algorytm nazywany „stacją rozrządową”, ponieważ jest w działaniu bardzo podobny do kolejowej stacji rozrządowej. Tak jak algorytm liczący wartość wyrażenia ONP, ten także działa na bazie stosu. Do konwersji używane są dwie zmienne (typu ciągu znakowego) — wejście oraz wyjście. Jest także stos przechowujący operatory niedodane jeszcze do wyjścia. W uproszczeniu, program czyta po kolei każdą literę i wykonuje operację zależną od tej litery.
Szczegóły algorytmu
- Póki zostały symbole do przeczytania wykonuj:
Przeczytaj symbol.- Jeśli symbol jest liczbą dodaj go do kolejki wyjście.
- Jeśli symbol jest funkcją włóż go na stos.
- Jeśli symbol jest znakiem oddzielającym argumenty funkcji (np. przecinek):
- Dopóki najwyższy element stosu nie jest lewym nawiasem, zdejmij element ze stosu i dodaj go do kolejki wyjście. Jeśli lewy nawias nie został napotkany oznacza to, że znaki oddzielające zostały postawione w złym miejscu lub nawiasy są źle umieszczone.
- Jeśli symbol jest operatorem, o1, wtedy:
1) dopóki na górze stosu znajduje się operator, o2 taki, że:
– o1 jest lewostronnie łączny i jego kolejność wykonywania jest mniejsza lub równa kolejności wyk. o2,
lub
– o1 jest prawostronnie łączny i jego kolejność wykonywania jest mniejsza od o2,
zdejmij o2 ze stosu i dołóż go do kolejki wyjściowej i wykonaj jeszcze raz 1)
2) włóż o1 na stos operatorów. - Jeżeli symbol jest lewym nawiasem to włóż go na stos.
- Jeżeli symbol jest prawym nawiasem to zdejmuj operatory ze stosu i dokładaj je do kolejki wyjście, dopóki symbol na górze stosu nie jest lewym nawiasem, kiedy dojdziesz do tego miejsca zdejmij lewy nawias ze stosu bez dokładania go do kolejki wyjście. Teraz, jeśli najwyższy element na stosie jest funkcją, także dołóż go do kolejki wyjście. Jeśli stos zostanie opróżniony i nie napotkasz lewego nawiasu, oznacza to, że nawiasy zostały źle umieszczone.
- Jeśli nie ma więcej symboli do przeczytania, zdejmuj wszystkie symbole ze stosu (jeśli jakieś są) i dodawaj je do kolejki wyjścia. (Powinny to być wyłącznie operatory, jeśli natrafisz na jakiś nawias oznacza to, że nawiasy zostały źle umieszczone.)
Przykład
Wejście 3+4×2/(1−5)^2
Przeczytaj „3”
Dodaj „3” do wyjścia
Wyjście: 3
Przeczytaj „+”
Włóż „+” na stos
Wyjście: 3
Stos: +
Przeczytaj „4”
Dodaj „4” do wyjścia
Wyjście: 3 4
Stos: +
Przeczytaj „×”
Włóż „×” na stos
Wyjście: 3 4
Stos: + ×
Przeczytaj „2”
Dodaj „2” do wyjścia
Wyjście: 3 4 2
Stos: + ×
Przeczytaj „/”
Zdejmij „×” ze stosu i dodaj do wyjścia, włóż „/” na stos
Wyjście: 3 4 2 ×
Stos: + /
Przeczytaj „(„
Włóż „(” na stos
Wyjście: 3 4 2 ×
Stos: + / (
Przeczytaj „1”
Dodaj „1” do wyjścia
Wyjście: 3 4 2 × 1
Stos: + / (
Przeczytaj „−”
Włóż „−” na stos
Wyjście: 3 4 2 × 1
Stos: + / ( −
Przeczytaj „5”
Dodaj „5” do wyjścia
Wyjście: 3 4 2 × 1 5
Stos: + / ( −
Przeczytaj „)”
Zdejmij „−” ze stosu i dodaj do wyjścia, zdejmij „(” ze stosu
Wyjście: 3 4 2 × 1 5 −
Stos: + /
Przeczytaj „^”
Włóż „^” na stos
Wyjście: 3 4 2 × 1 5 −
Stos: + / ^
Przeczytaj „2”
Dodaj „2” do wyjścia
Wyjście: 3 4 2 × 1 5 − 2
Stos: + / ^
Koniec wyrażenia
Zdejmij stos na wyjście
Wyjście: 3 4 2 × 1 5 − 2 ^ / +
Zamiana wyrażenia algebraicznego zapisanego w notacji infiksowej na postać postfiksową (ONP)

Gdy wczytany element jest:
- stałą lub nazwą zmiennej, to przesyłamy go na wyjście.
- ( to dopisujemy go na stos.
- ) to odczytaj ze stosu i prześlij na wyjście wszystkie operatory aż do nawiasu (, który należy odczytać, ale nie wysyłać na wyjście.
+, −, ×, /, %, ^. Jeżeli priorytet operatora wczytywanego jest wyższy od priorytetu operatora znajdującego się w wierzchołku stosu lub stos jest pusty, to dopisz do stosu operator, a w przeciwnym razie odczytaj i prześlij na wyjście kolejne operatory z wierzchołka stosu o priorytecie większym lub równym priorytetowi wczytanego operatora, po czym wpisz do stosu operator.
Na koniec, gdy wszystkie elementy zostały wczytane należy zdjąć wszystkie operatory ze stosu i przesłać je na wyjście.
Przykład :
Wyrażenie: 12 + a × (b × c + d / e)
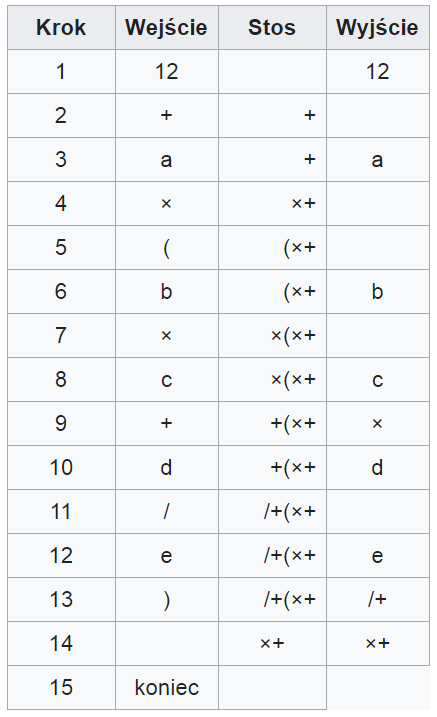
ONP: 12 a b c × d e / + × +
[źródło: Wikipedia]