W zbiorze tworzymy kopiec, a następnie dokonujemy jego rozbioru. W wyniku wykonania tych dwóch operacji zbiór zostanie posortowany.
Specyfikacja problemu
Dane wejściowe
d[ ] – Zbiór zawierający elementy do posortowania, które są numerowane począwszy od 1.
n – Ilość elementów w zbiorze, n ∈ N
Dane wyjściowe
d[ ] – Zbiór zawierający elementy posortowane rosnąco
Zmienne pomocnicze i funkcje
Twórz_kopiec – procedura budująca kopiec z elementów zbioru d[ ]. Kopiec powstaje w zbiorze d[ ].
Rozbierz_kopiec – procedura dokonująca rozbioru kopca utworzonego w zbiorze d[ ]. Wynik rozbioru trafia z powrotem do zbioru d[ ].
Lista kroków
K01: Twórz_kopiec
K02: Rozbierz_kopiec
K03: Zakończ algorytm
Ponieważ sortowanie przez kopcowanie składa się z dwóch następujących bezpośrednio po sobie operacji o klasie czasowej złożoności obliczeniowej O(n log n), to dla całego algorytmu klasa złożoności również będzie wynosić O(n log n).
int main()
{
const int N = 20; // liczebność zbioru
int d[N + 1],i,j,k,m,x;
srand((unsigned)time(NULL));
// Wypełniamy tablicę liczbami pseudolosowymi i wyświetlamy je
for(i = 1; i <= N; i++)
{
d[i] = rand() % 100; cout << setw(4) << d[i];
}
cout << endl;
// Budujemy kopiec
for(i = 2; i <= N; i++) { j = i; k = j / 2; x = d[i]; while((k > 0) && (d[k] < x))
{
d[j] = d[k];
j = k; k = j / 2;
}
d[j] = x;
}
// Rozbieramy kopiec
for(i = N; i > 1; i–)
{
swap(d[1], d[i]);
j = 1; k = 2;
while(k < i) { if((k + 1 < i) && (d[k + 1] > d[k]))
m = k + 1;
else
m = k;
if(d[m] <= d[j]) break;
swap(d[j], d[m]);
j = m; k = j + j;
}
}
// Wyświetlamy wynik sortowania
cout << „Po sortowaniu:\n\n”;
for(i = 1; i <= N; i++) cout << setw(4) << d[i];
cout << endl;
return 0;
}
Tworzenie kopca
Kopiec jest drzewem binarnym, w którym wszystkie węzły spełniają następujący warunek (zwany warunkiem kopca):
Węzeł nadrzędny jest większy lub równy węzłom potomnym (w porządku malejącym relacja jest odwrotna – mniejszy lub równy).
Konstrukcja kopca jest nieco bardziej skomplikowana od konstrukcji drzewa binarnego, ponieważ musimy dodatkowo troszczyć się o zachowanie warunku kopca. Zatem po każdym dołączeniu do kopca nowego węzła, sprawdzamy odpowiednie warunki i ewentualnie dokonujemy wymian węzłów na ścieżce wiodącej od dodanego węzła do korzenia.
Przykład:
Skonstruować kopiec z elementów zbioru {7 5 9 6 7 8 10}


Charakterystyczną cechą kopca jest to, iż korzeń zawsze jest największym (w porządku malejącym najmniejszym) elementem z całego drzewa binarnego.
Algorytm budowy kopca
Poniżej przedstawiamy algorytm konstrukcji kopca z elementów zbioru.
Specyfikacja problemu
Dane wejściowe
d[ ] – Zbiór zawierający elementy do wstawienia do kopca. Numeracja elementów rozpoczyna się od 1.
n – Ilość elementów w zbiorze, n ∈ N
Dane wyjściowe
d[ ] – Zbiór zawierający kopiec
Zmienne pomocnicze
i – zmienna licznikowa pętli umieszczającej kolejne elementy zbioru w kopcu, i ∈ N, i ∈ {2,3,…,n}
j,k – indeksy elementów leżących na ścieżce od wstawianego elementu do korzenia, j,k ∈ C
x – zmienna pomocnicza przechowująca tymczasowo element wstawiany do kopca
Lista kroków
K01: Dla i = 2, …, n:
wykonuj kroki K02…K05
K02: j ← i; k ← j div 2
K03: x ← d[i]
K04: Dopóki (k > 0) ∧ (d[k] < x):
wykonuj:
d[j] ← d[k]
j ← k
k ← j div 2
K05: d[j] ← x
K06: Zakończ
Algorytm tworzy kopiec w tym samym zbiorze wejściowym d[ ]. Nie wymaga zatem dodatkowych struktur danych i ma złożoność pamięciową klasy O(n).
Pętla nr 1 wyznacza kolejne elementy wstawiane do kopca. Pierwszy element pomijamy, ponieważ zostałby i tak na swoim miejscu. Dlatego pętla rozpoczyna wstawianie od elementu nr 2.
Wewnątrz pętli nr 1 inicjujemy kilka zmiennych:
j – pozycja wstawianego elementu (liścia)
k – pozycja elementu nadrzędnego (przodka)
x – zapamiętuje wstawiany element
Następnie rozpoczynamy pętlę warunkową nr 2, której zadaniem jest znalezienie w kopcu miejsca do wstawienia zapamiętanego elementu w zmiennej x. Pętla ta wykonuje się do momentu osiągnięcia korzenia kopca (k = 0) lub znalezienia przodka większego od zapamiętanego elementu. Wewnątrz pętli przesuwamy przodka na miejsce potomka, aby zachować warunek kopca, a następnie przesuwamy pozycję j na pozycję zajmowaną wcześniej przez przodka. Pozycja k staje się pozycją nowego przodka i pętla się kontynuuje. Po jej zakończeniu w zmiennej j znajduje się numer pozycji w zbiorze d[ ], na której należy umieścić element w x.
Po zakończeniu pętli nr 1 w zbiorze zostaje utworzona struktura kopca.
int main()
{
const int N = 31; // liczba elementów
int d[N + 1],i,j,k,x;
srand((unsigned)time(NULL));
// Inicjujemy zbiór d[] liczbami pseudolosowymi od 0 do 9
for(i = 1; i <= N; i++) d[i] = rand() % 10;
// Budujemy kopiec
for(i = 2; i <= N; i++) { j = i; k = j / 2; x = d[i]; while((k > 0) && (d[k] < x))
{
d[j] = d[k];
j = k; k = j / 2;
}
d[j] = x;
}
// Prezentujemy wyniki
x = (N + 1) / 2; k = 2;
for(i = 1; i <= N; i++)
{
for(j = 1; j <= x – 1; j++) cout << ” „;
cout << d[i];
for(j = 1; j <= x; j++) cout << ” „;
if(i + 1 == k)
{
k += k; x /= 2; cout << endl;
}
}
// Gotowe
cout << endl << endl;
return 0;
}
Rozbiór kopca
W tym rozdziale nauczymy się rozbierać kopiec. Zasada jest następująca:
Zamień miejscami korzeń z ostatnim liściem, który wyłącz ze struktury kopca. Elementem pobieranym z kopca jest zawsze jego korzeń, czyli element największy.
Jeśli jest to konieczne, przywróć warunek kopca idąc od korzenia w dół.
Kontynuuj od kroku 1, aż kopiec będzie pusty.
Przykład:
Dokonaj rozbioru następującego kopca:
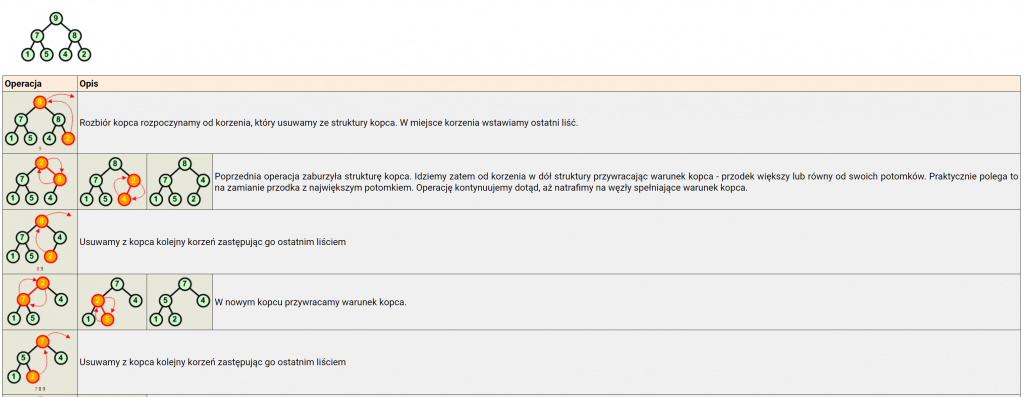

Operację rozbioru kopca można przeprowadzić w miejscu. Jeśli mamy zbiór d[ ] ze strukturą kopca, to idąc od końca zbioru (ostatnie liście drzewa) w kierunku początku zamieniamy elementy z pierwszym elementem zbioru (korzeń drzewa), a następnie poruszając się od korzenia w dół przywracamy warunek kopca w kolejno napotykanych węzłach.
Specyfikacja problemu
Dane wejściowe
d[ ] – Zbiór zawierający poprawną strukturę kopca. Elementy są numerowane począwszy od 1.
n – Ilość elementów w zbiorze, n ∈ N
Dane wyjściowe
d[ ] – Zbiór zawierający elementy pobrane z kopca ułożone w porządku rosnącym
Zmienne pomocnicze
i – zmienna licznikowa pętli pobierającej kolejne elementy z kopca, i ∈ N, i ∈ {n,n-1,…,2}
j,k – indeksy elementów leżących na ścieżce w dół od korzenia, j,k ∈ N
m – indeks większego z dwóch elementów potomnych, m ∈ N
Lista kroków
K01: Dla i = n, n – 1, …, 2:
wykonuj kroki K02…K08
K02: d[1] ↔ d[i]
K03: j ← 1; k ← 2
K04: Dopóki (k < i): wykonuj kroki K05…K08 K05: Jeżeli (k + 1 < i) ∧ (d[k + 1] > d[k]),
to m ← k + 1
inaczej m ← k
K06: Jeżeli d[m] ≤ d[j],
to wyjdź z pętli K04
i kontynuuj następny obieg K01
K07: d[j] ↔ d[m]
K08: j ← m; k ← j + j
K09: Zakończ
Rozbiór kopca wykonywany jest w dwóch zagnieżdżonych pętlach. Pętla nr 1 zamienia miejscami kolejne liście ze spodu drzewa z korzeniem. Zadaniem pętli nr 2 jest przywrócenie w strukturze warunku kopca.
Pętla nr 1 przebiega wstecz indeksy elementów zbioru d[ ] poczynając od indeksu n a kończąc na indeksie 2. Element i-ty jest wymieniany z korzeniem kopca. Po tej wymianie rozpoczynamy w pętli nr 2 przeglądanie drzewa od korzenia w dół. Zmienna j przechowuje indeks przodka, zmienna k przechowuje indeks lewego potomka. Pętla nr 2 kończy się, gdy węzeł j-ty nie posiada potomków. Wewnątrz pętli wyznaczamy w zmiennej m indeks większego z dwóch węzłów potomnych. Następnie sprawdzamy, czy w węźle nadrzędnym j-tym jest zachowany warunek kopca. Jeśli tak, to następuje wyjście z pętli nr 2. W przeciwnym razie zamieniamy miejscami węzeł nadrzędny j-ty z jego największym potomkiem m-tym i za nowy węzeł nadrzędny przyjmujemy węzeł m-ty. W zmiennej k wyznaczamy indeks jego lewego potomka i kontynuujemy pętlę nr 2.
Po wyjściu z pętli nr 2 zmniejszamy zmienną i o 1 – przenosimy się do kolejnego, ostatniego liścia drzewa i kontynuujemy pętlę nr 1.
W celu wyznaczenia klasy złożoności obliczeniowej algorytmu rozbioru kopca zauważamy, iż pętla zewnętrzna nr 1 wykona się n – 1 razy, a w każdym obiegu tej pętli pętla wewnętrzna wykona się maksymalnie log2n razy. Daje to zatem górne oszacowanie O(n log n) w przypadku pesymistycznym oraz O(n) w przypadku optymistycznym, który wystąpi tylko wtedy, gdy zbiór d[ ] będzie zbudowany z ciągu tych samych elementów.
#include <iostream>
#include <iomanip>
#include <cstdlib>
#include <time.h>
using namespace std;
int main()
{
const int N = 15; // liczba elementów
int d[N + 1],i,j,k,m,x;
srand((unsigned)time(NULL));
// W zbiorze d konstruujemy kopiec
d[1] = 9;
for(i = 2; i <= N; i++) d[i] = rand() % (d[i / 2] + 1);
// Prezentujemy kopiec
for(i = 1; i <= N; i++) cout << setw(2) << d[i];
cout << endl << endl;
x = (N + 1) / 2; k = 2;
for(i = 1; i <= N; i++)
{
for(j = 1; j < x; j++) cout << " ";
cout << d[i];
for(j = 1; j <= x; j++) cout << " ";
if(i + 1 == k)
{
k += k; x /= 2; cout << endl;
}
}
// Rozbieramy kopiec
for(i = N; i > 1; i--)
{
swap(d[1], d[i]);
j = 1; k = 2;
while(k < i)
{
if((k + 1 < i) && (d[k + 1] > d[k]))
m = k + 1;
else
m = k;
if(d[m] <= d[j]) break;
swap(d[j], d[m]);
j = m; k = j + j;
}
}
// Wyświetlamy wynik rozbioru kopca
cout << endl << "Zbior wyjsciowy po rozbiorze kopca:\n\n";
for(i = 1; i <= N; i++) cout << setw(2) << d[i];
cout << endl << endl;
// Gotowe
return 0;
}